Dynamically Generated Subtracting Integers Worksheet
Subtracting Integers Quiz – Word Problems
What is 7 − 3?
Looking for an engaging and effective way to teach your students or children how to subtract integers? Our subtracting integers worksheet collection is designed to help learners of all levels practice and master this essential algebraic skill. The worksheets cover a wide range of difficulty, from basic subtraction of positive integers to more complex operations involving negative numbers. Each worksheet includes 15 word problems, offering real-world applications that help students understand how subtraction works beyond just numbers on a page.
The worksheets are available in a downloadable PDF format, making them perfect for printing and offline practice. Additionally, the subtracting integers worksheet answers are provided, so students can check their work and correct mistakes. These exercises focus on a variety of important skills, such as subtracting positive and negative integers, subtracting negative from positive, and applying subtraction to real-world situations.
For those who prefer interactive learning, the online subtracting integers quiz/test is available, allowing students to practice directly on the web. The online quiz helps improve accuracy, speed, and problem-solving skills through immediate feedback. Each student can improve their understanding of negative numbers and complex subtraction operations, while the worksheets help solidify their learning at their own pace.
Whether for in-class practice or independent learning, this resource is an invaluable tool for teachers and parents looking to reinforce subtraction concepts in algebra.
Skills Focused: Subtraction of Positive Integers, Subtraction of Negative Integers, Subtracting Negative from Positive, Subtracting Positive from Negative, Application of Subtraction in Word Problems, Understanding Change in Values, Understanding Negative Numbers, Complex Subtraction Involving Negative Numbers, Negative Number Operations, Basic Subtraction Facts, Accuracy and Speed, Critical Thinking and Problem Solving, Number Line Understanding
How to Solve a Subtracting Integers Problem
What is −7 − 3?
Time needed: 2 minutes
Learn how to subtract fractions by converting mixed numbers to improper fractions and finding a common denominator.
- Understand the Problem
The problem is asking for the result of subtracting 3 from −7. You are given two numbers: −7 (minuend) and 3 (subtrahend). Since we’re subtracting a positive number, apply the ‘Keep-Change-Change’ rule.
- Apply the ‘Keep-Change-Change’ Rule
Keep the first number (−7) as it is. Change the subtraction sign (−) to addition (+). Change the sign of the second number (3) to its opposite, which is −3. The equation now becomes: −7 + (−3).
- Perform the Addition
Add the two numbers: −7 + (−3). Since both numbers are negative, add their absolute values and keep the negative sign. −7 + (−3) = −10.
- Verify the Result
To verify, reverse the operation: −10 + 3 = −7. This confirms the subtraction was correct.
- Final Answer
The final answer is −10.
What is the definition of an integer?
Integers are numbers without fractional or decimal parts. They include:
– All positive whole numbers (1, 2, 3, …)
– All negative whole numbers (−1, −2, −3, …)
– And zero (0)
In short, integers are the full set of numbers that can be written without a dot or fraction, stretching infinitely in both the positive and negative directions on a number line.
Mathematically, the set of integers is represented as:
… −3, −2, −1, 0, 1, 2, 3, …
Why are integers important in everyday math and algebra?
Whether you’re balancing a budget, calculating temperature changes, or solving for x in algebra, integers are everywhere.
Here’s why they matter:
Daily Life Applications: Think of your bank account. Deposits are positive integers, withdrawals are negative. The concept of “more” or “less” is tied directly to integers.
Direction & Movement: In physics or navigation, moving forward might be +5 meters and backward −3 meters, both are integers used to measure direction.
Algebra & Problem Solving: In equations and expressions, integers help represent unknowns and solve for variables. They’re the foundation for understanding more complex math like exponents, equations, and functions.
In essence, integers are the silent workhorses of math, forming the base layer that supports more advanced operations and real-world reasoning.
What is subtraction in the context of integers?
Subtraction of integers refers to finding the difference between two integers while considering their signs (positive or negative). The goal is to determine how much one integer is greater or smaller than the other.
Mathematically, subtracting integers means removing or taking away a certain value from another. The challenge arises from the fact that we are working with both positive and negative numbers, which behave differently depending on the situation.
The key to simplifying integer subtraction is recognizing that subtracting an integer is the same as adding its opposite (also known as the additive inverse).
For example, subtracting +5 is the same as adding −5.
How is subtracting different from adding integers?
At first glance, subtraction and addition might seem similar because they both involve combining or comparing numbers. However, they function very differently when it comes to integers.
Adding Integers: When you add two integers with the same sign, you simply add their absolute values and keep the sign. If they have different signs, you subtract the smaller absolute value from the larger one, and the result takes the sign of the larger number.
Example:
Adding positives: 3 + 5 = 8
Adding negatives: −4 + (−2) = −6
Different signs: 6 + (−4) = 2
Subtracting Integers: Subtraction, on the other hand, requires an extra step. You need to flip the sign of the second integer (the number you’re subtracting), then add it. This is where the “add the opposite” rule comes into play.
Example:
Simple subtraction: 7 − 3 = 4
Using the opposite: 7 − (−3) → 7 + 3 = 10
So, subtraction involves more than just combining numbers, it requires converting the operation to addition and adjusting the signs accordingly.
What is the “add the opposite” method?
The “add the opposite” method is the foundational rule for subtracting integers. It’s simple but powerful: subtracting an integer is the same as adding its opposite (also known as the additive inverse).
In practice:
Opposite of a positive number: The opposite of a positive integer is its negative counterpart. For example, the opposite of +5 is −5.
Opposite of a negative number: The opposite of a negative integer is its positive counterpart. For example, the opposite of −3 is +3.
So, instead of subtracting directly, we convert subtraction into an addition operation by changing the sign of the number we are subtracting. This makes it easier to apply the rules of addition, which are more straightforward.
Example:
Instead of calculating:
7 − 3, we can add the opposite of 3 (which is −3):
7 + (−3) = 4.
Why do we change subtraction to addition when dealing with integers?
The reason we change subtraction to addition when dealing with integers is rooted in the simplicity and consistency of the addition operation. Addition is much easier to handle because:
Adding two numbers is straightforward, whether they are positive or negative.
By converting subtraction to addition, we apply the same rules for all cases, whether we’re dealing with positive numbers, negative numbers, or a combination of both.
It’s all about making the math simpler and more manageable. Instead of dealing with complex subtraction rules for integers, we standardize the process by using the additive inverse (changing the sign of the number) and applying the well-known rules of addition.
What are the three steps of the Keep-Change-Change rule?
The “Keep-Change-Change” rule is a simple, step-by-step method that helps make subtracting integers much easier. It consists of three clear steps that simplify the process:
Keep the first number (minuend) the same.
Change the subtraction sign (−) to an addition sign (+).
Change the sign of the second number (subtrahend) to its opposite (additive inverse).
This rule turns the subtraction operation into an addition operation by adjusting only the signs, making it easier to work with integers.
Example:
Let’s say you need to solve: −7 − 3
Using the “Keep-Change-Change” rule:
Keep the first number (−7) as is.
Change the subtraction sign (−) to an addition sign (+).
Change the sign of the second number (3) to its opposite (−3).
Now, the equation looks like: −7 + (−3)
Finally, add the two numbers: −7 + (−3) = −10
How does Keep-Change-Change rule help simplify subtracting integers?
The “Keep-Change-Change” rule simplifies subtracting integers by eliminating the need for complex subtraction rules. Instead of thinking about how subtraction works with both positive and negative numbers, this rule turns the subtraction into a straightforward addition problem.
Here’s why it helps:
It reduces subtraction to a simple addition problem by changing the operation and adjusting the signs.
It avoids confusion, especially when dealing with negative numbers. Subtracting negative numbers can be tricky, but by turning it into addition, the process is the same as adding integers with opposite signs.
It provides a consistent method that works for all types of integer subtraction problems, whether you’re dealing with positive and negative numbers, or two negative integers.
The “Keep-Change-Change” rule is one of the most efficient ways to handle subtraction.
Can You Show a Step-by-Step Example?
Example: How do we solve −7 − 3?
Let’s break it down using the “Keep-Change-Change” rule.
We want to solve: −7 − 3
Step 1: Keep the first number the same
Start with the first number: −7. This stays as is.
Step 2: Change the subtraction sign to addition
Now, change the subtraction sign (−) to an addition sign (+).
So, we now have: −7 + 3
Step 3: Change the sign of the second number
The second number is 3, so we change its sign to its opposite, which is −3.
Now, the equation becomes: −7 + (−3)
Step 4: Add the two numbers
Finally, add −7 and −3. When adding two negative numbers, you simply add their absolute values and keep the negative sign.
−7 + (−3) = −10
So, the solution to −7 − 3 is −10.
Can Keep-Change-Change method be used for both positive and negative numbers?
Yes, the “Keep-Change-Change” method works for both positive and negative numbers! The rule doesn’t change based on the sign of the numbers involved. Whether you’re subtracting a positive or a negative integer, the steps stay the same, the subtraction sign gets changed to an addition sign, and the second number’s sign gets flipped.
Here are a few more examples to show how this method works:
Example 1: 5 − 3
Keep the first number: 5
Change the subtraction sign to addition: 5 +
Change the sign of 3: 5 + (−3)
Add the numbers: 5 + (−3) = 2
Example 2: −4 − (−6)
Keep the first number: −4
Change the subtraction sign to addition: −4 +
Change the sign of −6: −4 + 6
Add the numbers: −4 + 6 = 2
The beauty of the “Keep-Change-Change” rule is that it works consistently for any combination of integers, whether both numbers are positive, both negative, or one of each. This simplicity helps make integer subtraction much easier to understand and apply.
What happens when both integers are positive?
When both integers are positive, subtracting them works just like normal subtraction. You subtract the smaller number from the larger number, and the result remains positive (as long as the first number is larger than the second).
Example: 8 − 3
Subtract 3 from 8: 8 − 3 = 5
Since both numbers are positive, the result is also positive.
This is a straightforward subtraction problem, where you simply subtract the values and the result stays positive.
What if both are negative?
When both integers are negative, the subtraction works by treating it as addition of the opposite values. This is where the “add the opposite” rule comes into play. You’ll subtract the absolute values and keep the sign of the larger number (in terms of absolute value).
Example: −8 − (−3)
First, change the subtraction to addition: −8 + 3
Then, add the values: −8 + (−3) = −11
Here, both numbers are negative, but because you’re subtracting a negative number, it’s like adding the opposite. Since the result is still negative, the larger negative number stays in control of the sign.
How do we subtract a negative from a positive?
When you subtract a negative number from a positive number, it’s the same as adding the positive integer to the absolute value of the negative number. This is a critical point: subtracting a negative is like adding a positive.
Example: 5 − (−3)
Change the subtraction to addition: 5 + 3
Then, add the values: 5 + 3 = 8
In this case, subtracting −3 from 5 is the same as adding 3, which gives you a positive result.
What about subtracting a positive from a negative?
When you subtract a positive number from a negative number, you are essentially moving further into the negative side of the number line. The result will always be negative, and you add the absolute values together.
Example: −5 − 3
Simply add the absolute values: 5 + 3 = 8
Since both numbers are negative, the result is negative: −8
Here, you’re moving 3 steps further away from 0 in the negative direction, so the result is −8.
This breakdown of subtracting integers with the same or different signs should help clarify how the operations work depending on the sign of each number. 
How do you use a number line to subtract integers?
A number line is a useful tool for visualizing integer subtraction. It helps you see how numbers move in relation to each other, particularly when dealing with both positive and negative integers.
Here’s how it works:
Start by locating the first number (minuend) on the number line.
For subtraction, you’ll move in the opposite direction based on the number you’re subtracting (the subtrahend).
If you’re subtracting a positive number, you move to the left on the number line.
If you’re subtracting a negative number, you move to the right, because subtracting a negative is like adding the positive version of that number.
Using a number line provides a visual understanding of how subtraction moves numbers along the line, which can help clarify the process.
Why do we move left for positives and right for negatives?
The reason we move left for positive numbers and right for negative numbers is based on the direction of change on the number line:
Moving left means you’re decreasing the value. Since subtracting a positive number means you’re taking away from your current position, you move left (toward smaller values).
Moving right means you’re increasing the value. Subtracting a negative number is the same as adding the opposite, so you’re essentially moving in the positive direction, which is to the right on the number line.
It’s all about the direction of change:
Subtracting positive = move left.
Subtracting negative = move right.
Is subtraction of integers closed (closure property)?
No, integer subtraction is not closed.
The closure property states that if you subtract two integers, the result will always be an integer. This property holds true for addition and multiplication of integers, but not for subtraction.
For example, while subtracting integers like 8 − 3 = 5 is valid, subtraction of integers can also result in negative numbers or zero, and there is no guarantee that the operation will always result in an integer that behaves in the same way as addition or multiplication.
In other words, integer subtraction does not always preserve the “structure” of numbers in the same way addition and multiplication do.
What’s the identity property in subtraction?
In subtraction, the identity property is simple: subtracting zero leaves the number unchanged.
Identity property of subtraction: If you subtract zero from any integer, the result will be that integer itself.
Example:
5 − 0 = 5
−8 − 0 = −8
This is because zero has no effect when subtracted. It is the identity element for subtraction, unlike addition where the identity element is zero for addition (where adding zero doesn’t change the number).
What is the inverse property in subtraction?
The inverse property for subtraction can be thought of as subtracting a number’s opposite. When you subtract the opposite of a number, the result is double the original number.
In mathematical terms:
a − (−a) = a + a = 2a
This means that if you subtract a negative number from a positive number, you essentially add the number to itself.
Example:
5 − (−5) = 5 + 5 = 10
−3 − (−3) = −3 + 3 = 0
This is called the inverse property of subtraction because subtracting a negative number is equivalent to adding its positive counterpart, effectively doubling the original number or returning to zero.
Is subtraction commutative or associative?
Subtraction is not commutative.
Subtraction is not associative.
Commutative property: For an operation to be commutative, the order in which you perform the operation does not change the result. Subtraction does not satisfy the commutative property, because changing the order of subtraction leads to different results.
Example:
5 − 3 ≠ 3 − 5
5 − 3 = 2, but 3 − 5 = −2
So, subtraction is not commutative.
Associative property: For an operation to be associative, grouping of numbers doesn’t affect the result. Subtraction is not associative, meaning changing the grouping of numbers in subtraction will change the result.
Example:
(5 − 3) − 2 ≠ 5 − (3 − 2)
(5 − 3) − 2 = 2 − 2 = 0, but
5 − (3 − 2) = 5 − 1 = 4
So, subtraction is not associative either.
Summary of Properties
Closure: Integer subtraction is not closed. The result might not be consistent like addition or multiplication.
Identity Property: Subtracting 0 leaves the integer unchanged (e.g., 5 − 0 = 5).
Inverse Property: Subtracting a number’s opposite results in double the original number (e.g., 5 − (−5) = 10).
Commutative Property: Subtraction is not commutative. The order of subtraction affects the result.
Associative Property: Subtraction is not associative. Grouping changes the result.
These properties highlight how subtraction behaves differently compared to addition and multiplication. Understanding these helps clarify why integer subtraction doesn’t follow all the same rules.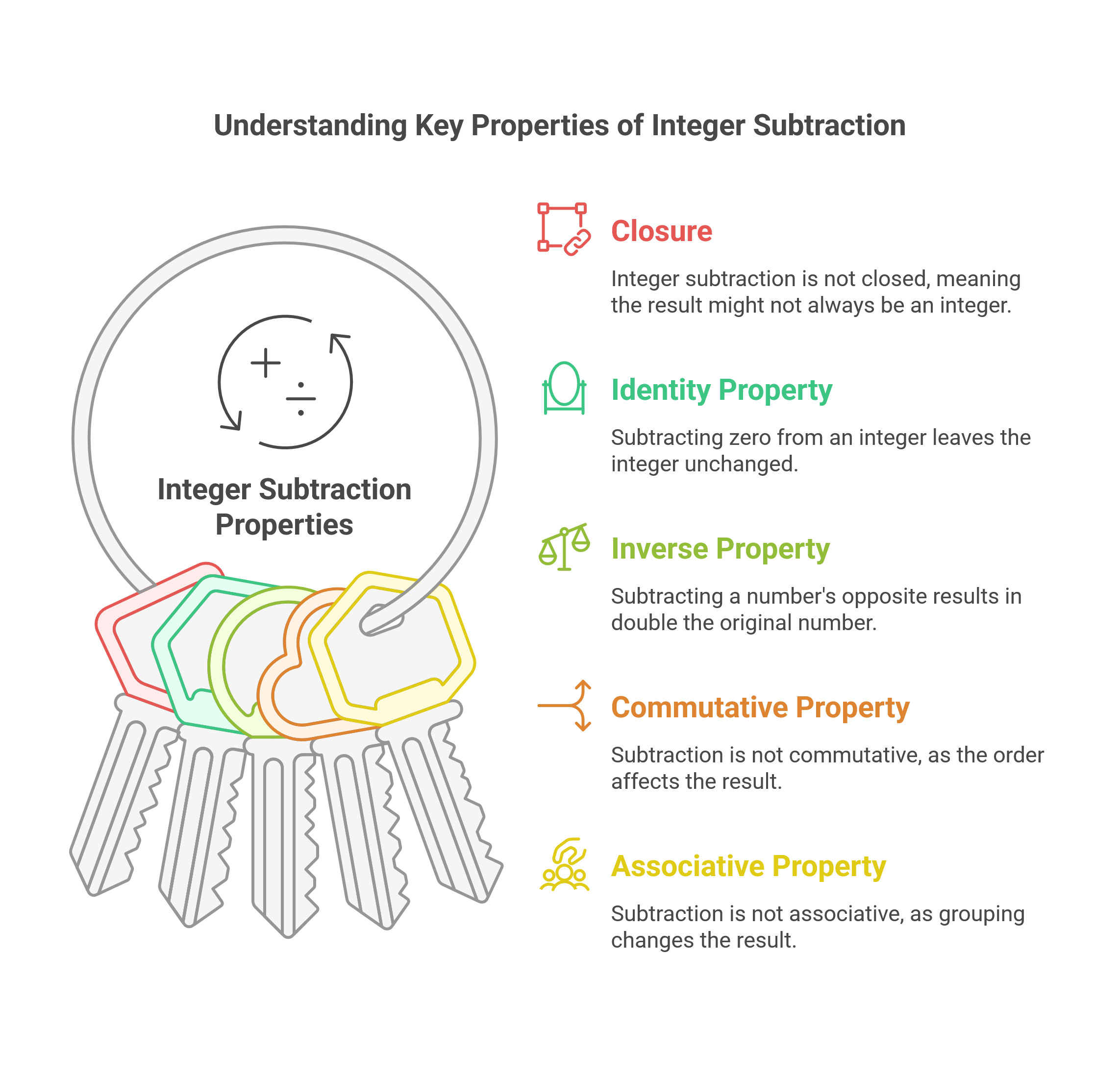
What is 13 − 8?
This is a straightforward positive minus positive subtraction.
Step 1: Start with 13.
Step 2: Subtract 8.
Step 3: The result is 5.
13 − 8 = 5
Since both numbers are positive, simply subtract the smaller number (8) from the larger number (13), and the result is positive.
How about (−39) − (−14)?
This is an example of subtracting a negative from a negative, which requires us to use the “add the opposite” rule.
Step 1: Start with −39.
Step 2: Change the subtraction to addition, and flip the sign of −14 to +14.
Step 3: Now, you’re adding −39 + 14.
−39 + 14 = −25
In this case, since −39 is more negative than +14, the result remains negative. So, (−39) − (−14) = −25.
How do we simplify −16 − 4?
This is a negative minus positive problem. You are subtracting a positive number from a negative number, which moves you further into the negative direction.
Step 1: Start with −16.
Step 2: Subtract 4.
Subtracting a positive number moves you left on the number line.
Step 3: Add −4 to −16.
−16 − 4 = −20
Here, subtracting 4 from −16 just means you move 4 more steps left on the number line, resulting in −20.
Example with large integers: 2 − (−88)
This is an example of subtracting a negative number from a positive number. Remember, subtracting a negative number is the same as adding that number’s positive counterpart.
Step 1: Start with 2.
Step 2: Change the subtraction to addition: 2 + 88.
Step 3: Add the numbers.
2 + 88 = 90
So, 2 − (−88) = 90. Subtracting −88 from 2 is like adding 88, which brings us to 90.





